Próximo: Acción de sobre el Arriba: La Geometría Proyectiva de Anterior: Motivación

Conceptos algebraicos básicos

Definición 2.1   Sea $V$un espacio vectorial sobre un cuerpo $\mathbb{F}$. Se dice que una aplicación

$$B\colon V\times V \rightarrow \mathbb{F}$$

es una forma bilineal si

$$\begin{array}{rcl} B(\lambda v+v',w) & = & \lambda B(v,w)+B(... ...\\ B(v, \lambda w+w') & = & \lambda B(v,w)+B(v,w') \end{array}$$

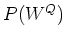
Para cualesquiera vectores $v,v',w,w'\in V$y cualquier escalar $\lambda\in\mathbb{F}$.

Definición 2.2   Una forma bilineal se dice simétrica (resp. antisimétrica) si $B(v,w)=B(w,v)$ (resp. $B(v,w)=-B(w,v)$) para cualesquiera vectores $v,w\in V$. El radical de una forma bilineal $B$es el conjunto de vectores $v$ tales que $B(v,w)=0$ para todo $w\in V$. Se llama nulidad a la dimensión del radical de $B$. Si la nulidad de una forma bilineal es cero, la forma se dice no degenerada.

Ejercicio 2.1 (10)   Sea $W$un espacio vectorial sobre $\mathbb{F}$, sea $W^*$su dual, y sea $V$el producto $W\times W^*$. Probar que la función

$$\omega\colon V\times V\rightarrow \mathbb{F}$$

definida por $\omega((v,f),(v',f')):=f'(v)-f(v')$ es una forma bilineal no degenerada y antisimétrica. La llamaremos forma canónica simpléctica sobre $V$.

Ejercicio 2.2 (*05)   Sea $V$un espacio vectorial de dimensión $n$sobre un cuerpo $\mathbb{F}$ con $p$  elementos. ¿Cuántas formas bilineales diferentes hay sobre $V$?

Ejercicio 2.3 (10)   Sea $V$un espacio vectorial de dimensión $n$ sobre un cuerpo $\mathbb{F}$. Demostrar que si fijamos una base de $V$, el conjunto de formas bilineales está en correspondencia biunívoca con el conjunto de las matrices $n\times n$ con entradas en $\mathbb{F}$. Además, la forma es simétrica si y sólo si la matriz es simétrica.

Definición 2.3   Sea $V$un espacio vectorial sobre un cuerpo $\mathbb{F}$. Una forma cuadrática sobre $V$es una función $Q\colon V\rightarrow\mathbb{F}$ tal que existe una forma bilineal $B$con $Q(v)=B(v,v)$  para todo $v\in V$.

Ejercicio 2.4 (15)   Probar que si $Q$es una forma cuadrática, existe una única forma bilineal simétrica $B$ tal que $Q(v)=B(v,v)$ para todo $v\in V$. Dar una fórmula para $B$en función de $Q$.

Definición 2.4   Una forma cuadrática $Q$sobre $\mathbb{R}^n$se dice, que es definida positiva (resp. definida negativa) si $Q(v)>0$ (resp. $Q(v)<0$) para todo vector no nulo $v\in V$.

Observación. Para realizar los ejercicios anteriores, hay que escribir una forma cuadrática sobre $\mathbb{R}^n$de la forma

$$Q(x_1\cdots ,x_n):=(x_1,\cdots x_n) \left ( \begin{array}{ccc} a_... ...\right ) \left ( \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right ) ,$$

Con $a_{ij}=a_{ji}$.

Sea $V$un espacio vectorial y sea $P(V)$su proyectivización. Si $Q$es una forma cuadrática sobre $V$y $v$ es un vector no nulo tal que $Q(v)=0$, entonces $Q(\lambda v)=0$ para cualquier escalar $\lambda$. Esto sugiere la siguiente definición:

Definición 2.5   Sea $V$un espacio vectorial y sea $P(V)$su proyectivización. Si $Q$es una forma cuadrática sobre $V$, la hipercuádrica proyectiva asociada a $Q$es el conjunto

$$\mathcal Q:=\{[v]\in P(V)\colon v\in V\setminus\{0\},Q(v)=0\}$$

Las hipercuádricas proyectivas sobre $\mathbb{R} P^2$se llaman cónicas. Si la forma bilineal simétrica asociada a $Q$es no degenerada, diremos que $\mathcal Q$es no degenerada o propia.

Puede pasar que la hipercuádrica proyectiva asociada a una forma cuadrática sea vacía. Por ejemplo si $Q(x_1,x_2,x_3)=x_1^2+x_2^2+x_3^2$, entonces $\mathcal Q\subset \mathbb{R} P^2$es el conjunto vacío.

Terminamos la sección demostrando el siguiente resultado importante:

Teorema 2.6   Si $\mathcal Q\in\mathbb{R}P^n$ es una hipercuádrica no degenerada, el conjunto formado por todos los hiperplanos tangentes a $\mathcal Q$ es una hipercuádrica no degenerada en el espacio dual $\mathbb{R}P^{n*}$.

Definición 2.7   La hipercuádrica proyectiva en $\mathbb{R}P^{n*}$ formada por el conjunto de todos los hiperplanos tangentes a una hipercuádrica no degenerada $\mathcal Q\subset \mathbb{R}P^n$ se llama la hipercuádrica dual de $\mathcal Q$ y será denotada por $\mathcal Q^*$.

Sea $Q\colon\mathbb{R}^{n+1}\rightarrow \mathbb{R}$ la forma cuadrática no degenerada asociada a $\mathcal Q$ y sea $B$ la forma bilineal simétrica que satisface $Q(v)=B(v,v)$. Definimos la aplicación

$$dQ\colon\mathbb{R}^{n+1}\rightarrow\mathbb{R}^{n+1*}$$

por la ecuación $dQ(v)(w)=2B(v,w)$

Ejercicio 2.5 (00)   Probar que $dQ$ es una aplicación lineal invertible.

Ejercicio 2.6 (10)   Sea $v\in\mathbb{R}^{n+1}$un vector no nulo que está sobre el cono $Q=0$. Probar que

$$\Pi_v:=\{w\in\mathbb{R}^{n+1}\colon dQ(v)(w)=0\}$$

es un hiperplano de $\mathbb{R}^{n+1}$ que pasa por el origen y es tangente al cono $Q=0$ en el punto $v$ Demostrar que si $\lambda$es un escalar no nulo entonces $\Pi_{\lambda v}=\Pi_v$.

Ejercicio 2.7 (05)   Demostrar que la hipercuádrica dual $\mathcal Q^*$es la imagen de $\mathcal Q$ mediante la transformación proyectiva inducida por $dQ$. Usar esto para demostrar el teorema 2.1.

Ejercicio 2.8 (10)   Estudiar la dualidad de las hipercuádricas degeneradas.

Próximo: Acción de sobre el Arriba: La Geometría Proyectiva de Anterior: Motivación